  
等级: 管理员
- 注册:
- 2021-5-10
- 曾用名:
|
本帖最后由 技术006 于 2021-10-21 13:41 编辑
为了方便用户进行线性代数与矢量分析,金字塔提供了一整套封装的高度矢量优化线性代数方面函数,用户可以不借助Python也可以在PEL中进行简易矩阵及向量计算。金字塔会根据用户CPU自动启用SSE,AVX,AVX-512指令集,以及高度并行化执行,可以发挥CPU最大利用率,执行效率大大提升。
使用事项说明
1、该类函数的向量及矩阵的输入参数只能是VARIABLE申明的数组类型,使用前应注意转换。相关的教程请参考 金字塔数组使用的高级编程技巧
2、函数计算需依赖科学计算组件,该组件您需要单独安装部署,使用前请先进行在线安装。
安装步骤 : PEL公式编辑器界面->插入菜单->安装扩展科学计算组件。
3、该类库函数还在不断扩充中,如果你有其他的功能函数需求,欢迎及时在本贴中提出,以便我们进行扩充安排。
函数说明(5.0 BETA3版本后支持)
1、Mfsum(X,N)
计算向量x的元素大小之和
函数实现功能: y=∑x
参数维度说明: x为向量(n*1)(矩阵也可以看做向量)
例:
[PEL] 复制代码 VARIABLE:x[]=0;
x:=c;
rets:Mfsum(x,5);
========================================
2、Mfxpy(x,y,alpha,n)
计算向量与标量的积,然后加到结果上
函数实现功能:y:=a*x+y
x : 向量
y : 向量(输出参数)
alpha : 标量
n : 指定向量x,y的元素个数
返回值 : 最终更新到向量y
例:
[PEL] 复制代码 alpha:=1;
VARIABLE : x[5]=(0,1,2,3,4);
VARIABLE : y[5]=(1,2,3,4,5);
If IsLastbar Then
Begin
MFXPY(x,y,ALPHA,5);
for i = 1 to 5 do
msgout(1,numtostr(y,0));//结果将输出 1,3,5,7,9
End
========================================
3、Mfdot(x,y,n)
计算向量-向量的点乘
函数实现功能公式:
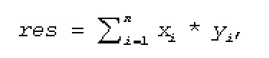
x : 向量
y : 向量
n:向量x,y数量
例:
[PEL] 复制代码 VARIABLE : x[5]=(0,1,2,3,4);
VARIABLE : y[5]=(1,2,3,4,5);
RETS:MFDOT(x,y,5);//结果将输出40
========================================
4、Mfnrm2(x,n)
计算一个向量的欧几里得范数(Euclidean norm)
函数实现功能:res = ||x||
x:向量
n:向量x个数
例:
[PEL] 复制代码 VARIABLE : x[5]=(1,2,3,4,5);
RETS:MFNRM2(x,5); //结果将输出 7.416
========================================
5、Mfscal(x,a,n)
计算向量和标量的乘积 函数实现功能:x=a*x x : 向量(输入/输出参数) a : 标量a n: 向量x个数 返回值:最终更新到向量x
例: [PEL] 复制代码 VARIABLE : x[5]=(1,2,3,4,5);
a:=0.1;
If IsLastbar Then
Begin
MFSCAL(x,a,5);
for i = 1 to 5 do
Msgout(1,numtostr(x,1)); //结果将输出 0.1,0.2,0.3,0.4,0.5
End
========================================
6、Mfswap(x,y,n)
交换向量值, 完成向量x和y的交换 x : 向量 y : 向量 n:向量x,y数量
例: [PEL] 复制代码 VARIABLE : x[5]=(0,1,2,3,4);
VARIABLE : y[5]=(1,2,3,4,5);
If IsLastbar Then
Begin
Mfswap(x,y,5);
for i = 1 to 5 do
msgout(1,numtostr(y,0)); //输出交换后的y数组
End
========================================
7、mfamax(x,n)
找到绝对值最大的元素的索引 x: 向量 n: 向量x个数 返回值:基于1索引的向量元素位置
例: [PEL] 复制代码 VARIABLE : x[5]=(0,1,2,3,4);
Rets:MFAMAX(x,5); //结果将返回5
========================================
8、Mfamin(x,n)
找到绝对值最小的元素的索引 x: 向量 n: 向量x个数 返回值:基于1索引的向量元素位置
例:见Mfamax函数
========================================
9、mfAdd(a,b,r,n)
向量元素相加 a : 向量 b : 向量 r:向量(输出值) n: 向量a,b,r个数
例: [PEL] 复制代码 VARIABLE : a[5]=(1,2,3,4,5);
VARIABLE : b[5]=(1,2,3,4,5);
VARIABLE : r[5]=0;
If IsLastbar Then
Begin
MFADD(a,b,r,5);
for i = 1 to 5 do
msgout(1,numtostr(r,0)); //结果将返回2,4,6,8,10
End
========================================
10、MfSub(a,b,r,n)
向量元素相减 a : 向量 b : 向量 r : 向量(输出值) n: 向量a,b,r个数
例:见mfAdd函数
========================================
11、MfMul(a,b,r,n)
向量元素相乘 a : 向量 b : 向量 r:向量(输出值) n: 向量a,b,r个数
例:见mfAdd函数
========================================
12、MfDiv(a,b,r,n)
向量元素相除 a : 向量 b : 向量 r:向量(输出值) n: 向量a,b,r个数
例:见MfAdd函数
========================================
13、Mfgemv(a,x,y,t,m,n,alpha,beta)
矩阵与向量的乘积 函数实现功能: t =0 y := alpha*A*x + beta*y, t =1 y := alpha*A'*x + beta*y, t =2 y := alpha*conjg(A')*x + beta*y, a : m*n的矩阵 x : 向量 y : 向量(输入和输出参数) m : 矩阵A的行数 n : 矩阵A的列数(向量x维度) alpha : 标量 beta : 标量 返回值:最终更新到向量y
例: [PEL] 复制代码 m:=2;//矩阵行数
n:=5;//矩阵列数
alpha:=1;
mbeta:=1;
VARIABLE : a[m*n]=( 0,1,2,3,4,
5,6,7,8,9 ); //定义一个2行5列矩阵
VARIABLE : x[n]=(1,2,3,4,5); //向量数组
VARIABLE : y[m]=0;
If IsLastbar Then
Begin
//2*5的矩阵与5*1的向量相乘
MFGEMV(a,x,y,0,m,n,alpha,mbeta);
for i = 1 to m do
msgout(1,numtostr(y,0)); //结果将输出40, 115
End ========================================
14、Mfger(x,y,a,m,n,alpha)
矩阵的一阶更新(矩阵-向量乘积) 函数实现功能:A := alpha*x*y'+ A, x : 向量(m行) y : 向量(n列) a : m×n 的矩阵(输入和输出参数) m : 矩阵A的行数 n : 矩阵A的列数 alpha : 标量 返回值:最终更新到矩阵a
例: [PEL] 复制代码 m:=2;//矩阵行数
n:=5;//矩阵列数
alpha:=1;
VARIABLE : x[m]=(1,2);
VARIABLE : y[n]=(2,3,4,5,6);
VARIABLE : a[m*n]=( 1,1,1,1,1,
1,1,1,1,1 ); //定义一个2行5列矩阵
If IsLastbar Then
Begin
//5*1向量乘以1*5向量,加上5*5矩阵
MFGER(x,y,a,m,n,alpha);
for i = 1 to m*n do
msgout(1,numtostr(a,0));
End 结果将输出矩阵为 3 4 5 6 7
5 7 9 11 13 ======================================== 15、Mfgemm(A,B,C,alpha,beta,m,n,k)
矩阵与矩阵乘积
函数实现功能:C := alpha*op(A)*op(B) + beta*C, A: 矩阵 B: 矩阵 C:矩阵(输入和输出参数) alpha: 标量 beta : 标量 m:矩阵A和矩阵C的行数 n:矩阵B和矩阵C的列数 k:矩阵A的列数和矩阵B的行数 返回值:最终更新到矩阵C 例: [PEL] 复制代码 m:=2;//矩阵A和矩阵C的行数
n:=3;//矩阵B和矩阵C的列数
k:=2;//矩阵A的列数和矩阵B的行数
alpha:=1;
betas:=1;
VARIABLE : a[m*n]=(1,2,3, 4,5,6); //矩阵维度 2*3
VARIABLE : b[n*k]=(1,1, 1,1, 1,1); //矩阵维度 3*2(计算时候转置)
VARIABLE : x[m*k]=(0,1, 2,3); //矩阵维度 2*2
If IsLastbar Then
Begin
MFGEMM(a,b,x,alpha,betas,m,n,k);
for i = 1 to m*k do
msgout(1,numtostr(x,0));
End
6 7
1718
========================================
16、Mffft(X,Y,N,T)
快速傅立叶变换 X: 输入源向量数组 Y: 输出向量数组,以复数方式返回(由2个数字组成),因此数组申明大小必须为X的2倍 N: X向量变换源数组大小 T:0向前变换 1向后变换
例: [PEL] 复制代码 n:=16; //16点信号变换
VARIABLE : x[n]=(15, 32, 9, 222, 118, 151, 5, 7, 56, 233, 56, 121, 235, 89, 98, 111);
VARIABLE : y[n*2]=0; //以复数方式返回结果,因此需要2倍容量
If IsLastbar Then
Begin
MFFFT(x,y,n,0);
for i = 1 to n*2 do
msgout(1,numtostr(y,3));
End
|
|